Esta medida de dispersión no es desconocida para nosotros, pues ya hemos trabajado con la noción del valor mayor y menor de un conjunto de datos. Es conveniente definir el rango como tal:
El rango o amplitud es una medida de dispersión que se define como la diferencia entre el dato mayor y menor valor en un conjunto de datos.
Debido a que el Rango se calcula a partir de dos valores, esta medida de dispersión no nos aporta muchos elementos para determinar si los datos que se encuentren en ese intervalo tienen mucha o po0ca variabilidad; es más, el rango en determinado momento puede depender de la inclusión de más valores al conjunto de datos.
Para comprender la utilidad del rango, analizaremos la siguiente situación
Ejemplo:
Matilda quien es ahorrativa, registró sus datos escolares durante un mes, se encontraba de la siguiente manera:

Analizando estos datos, nos damos cuenta que el valor mínimo es 16 y el valor máximo es 25. Por tanto, los demás valores se encuentran distribuidos en ese intervalo.
Por lo tanto 9 es el valor del rango del conjunto de datos del ahorro de Matilda.


 El valor de la media aritmética de este conjunto de datos es el siguiente:
El valor de la media aritmética de este conjunto de datos es el siguiente:
 Para hacer el cálculo de la desviación media, se construye la siguiente tabla auxiliar:
Para hacer el cálculo de la desviación media, se construye la siguiente tabla auxiliar: Retomando la fórmula de la desviación media y calculando los valores:
Retomando la fórmula de la desviación media y calculando los valores: Como habrás notado, aún con pocos datos, el cálculo de la desviación media no resulta del todo sencilla y el cálculo se vuelve más laborioso en cuanto más crece el número de datos.
Como habrás notado, aún con pocos datos, el cálculo de la desviación media no resulta del todo sencilla y el cálculo se vuelve más laborioso en cuanto más crece el número de datos.
 Un grupo de amigos registra su consumo mensual de crédito en su celular, con la finalidad de incluirse en un plan tarifario. Los datos registrados son los siguientes:
Un grupo de amigos registra su consumo mensual de crédito en su celular, con la finalidad de incluirse en un plan tarifario. Los datos registrados son los siguientes:


 Se realiza el cálculo de las columnas correspondientes:
Se realiza el cálculo de las columnas correspondientes:
 De igual forma, se puede calcular a partir de la fórmula alternativa:
De igual forma, se puede calcular a partir de la fórmula alternativa: Para el ejemplo del gasto mensual en telefonía celular, los datos tienen la siguiente varianza:
Para el ejemplo del gasto mensual en telefonía celular, los datos tienen la siguiente varianza:


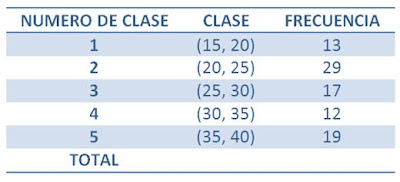
 La tabla anterior representa las cabezas de ganado del rancho “Laguna Seca”.
La tabla anterior representa las cabezas de ganado del rancho “Laguna Seca”.


 Donde, como sabemos:
Donde, como sabemos:
 En lo que representa al valor máximo y mínimo de los datos, la distribución puede adoptar las siguientes formas:
En lo que representa al valor máximo y mínimo de los datos, la distribución puede adoptar las siguientes formas:
 Los diferentes tipos de asimetría, se pueden visualizar en las siguientes imágenes:
Los diferentes tipos de asimetría, se pueden visualizar en las siguientes imágenes:

 Donde:
Donde:



 El valor de la media aritmética, se calcula de manera inmediata:
El valor de la media aritmética, se calcula de manera inmediata: Es ejercicio para el estudiante, verificar el cálculo de la desviación estándar.
Es ejercicio para el estudiante, verificar el cálculo de la desviación estándar. El valor calculado se confronta con 0.263, resultando que -0.5454<0.263; por tanto la distribución es platicúrtica o achatada.
El valor calculado se confronta con 0.263, resultando que -0.5454<0.263; por tanto la distribución es platicúrtica o achatada. Donde:
Donde:

 La ecuación anterior, como te habrás dado cuenta, corresponde el valor de la media aritmética.
La ecuación anterior, como te habrás dado cuenta, corresponde el valor de la media aritmética. Donde:
Donde: Realizando las sustituciones correspondientes, el valor del momento a la media para r = 0 y r = 1, es el siguiente:
Realizando las sustituciones correspondientes, el valor del momento a la media para r = 0 y r = 1, es el siguiente: Lo cual corresponde al valor de la varianza y se conoce así como momento de la varianza o de orden 2.
Lo cual corresponde al valor de la varianza y se conoce así como momento de la varianza o de orden 2.

 Respecto a este tipo de momentos, no nos relaciona alguna de las medidas de tendencia central y de dispersión estudiadas.
Respecto a este tipo de momentos, no nos relaciona alguna de las medidas de tendencia central y de dispersión estudiadas.